Tolka output från regressionsanalys

Hur ska man tolka en regressionsanalys? Det beror givetvis på frågeställningen, teorin, datans kvalitet, med mera. Men man måste också veta hur man ska tolka de olika siffrorna som Stata spottar ut. Dem ska vi titta på i det här inlägget.

Nedan är resultatet från en analys av en amerikansk enkätundersökning från 2018. Den beroende variabeln är hur mycket den svarande tjänar, i dollar, på ett år. Den oberoende variabeln är hur månag timmar den svarande arbetade föregående vecka. I den riktiga undersökningen är det tusentals svarande, men jag har här slumpmässigt valt ut 46 personer för att resultatet ska bli lite mer överskådligt.

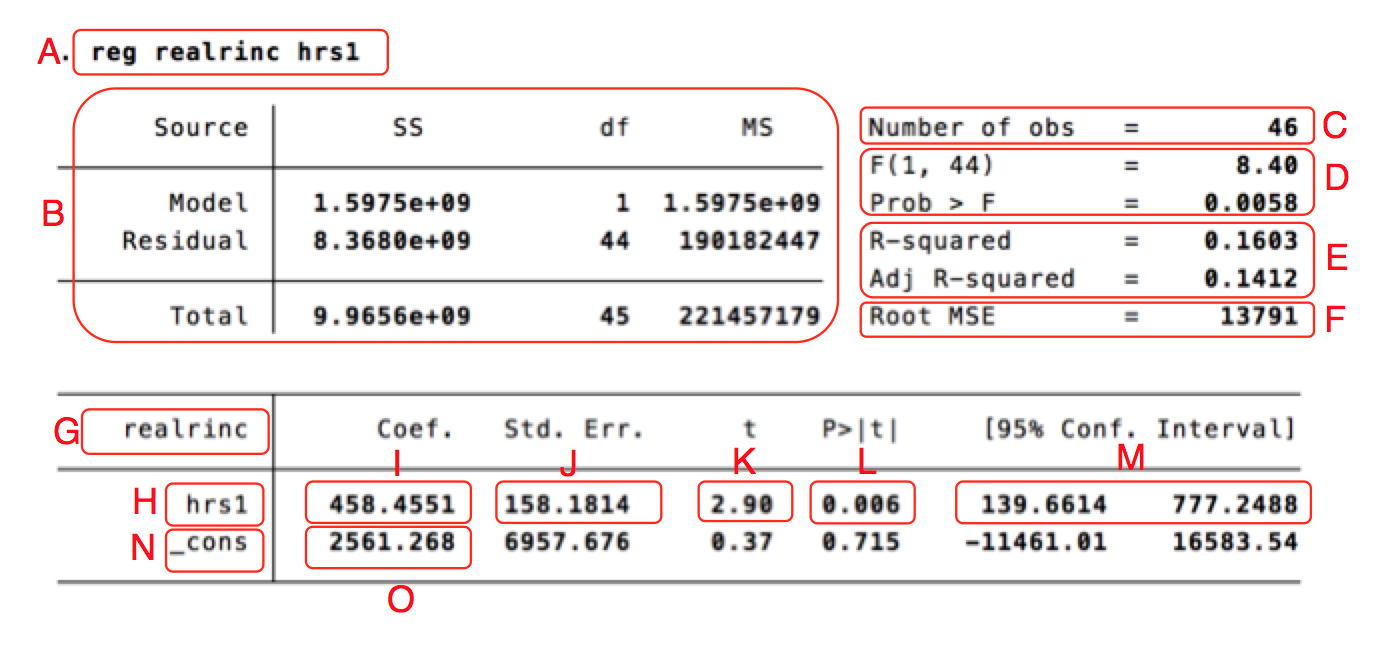
Bokstav	Betydelse
A	En kopia av regressionskommandot som analysen bygger på.
B	Summerande värden som används för att räkna ut andra värden i outputen. Den här delen tolkas sällan.
C	Antal observationer som ingick i analysen: 46 stycken. Kallas också N-talet.
D	F-värdet (8.40). Det är ett sammanfattande mått som används för att testa hypotesen att någon av variablerna i modellen har en effekt på den beroende variabeln. Vi får också ett signifikanstest (Prob > F), som visar om F-värdet är signifikant. I det här fallet är F-värdet signifikant på 99%-nivån, eftersom värdet är under 0.01. Det finns alltså goda grunder att tro att minst en av de oberoende variablerna i modellen har en effekt (i det här fallet har vi dock bara en oberoende).
E	$R^2$-värdet, som visar andelen förklarad varians. Det vill säga, hur mycket av variationen i den beroende variabeln kan förklaras av variationen i den oberoende variabeln? Det vill säga, hur mycket av variationen i inkomst förklaras av hur mycket folk jobbar? I det här fallet är värdet 0.1603, vilket kan tolkas som att 16% av variationen i inkomst förklaras av variationen i arbetstid. Vi får också ut "adjusted R-square" som är ett anpassat $R^2$-mått. Det vanliga måttet kan bara gå uppåt när man lägger till fler oberoende variabler, även om de inte har någon förklaringskraft. Med adjusted r-square blir det "minuspoäng" för varje ny variabel som läggs till, för att göra jämförelser mellan modeller mer rättvisa.
F	"Root Mean Square Error", ett mått på hur nära modellens gissningar ligger verkligheten, ett typiskt fel ungefär. I det här fallet är det 13791 dollar. Fångar i princip upp samma saker som $R^2$, fast det här måttet är uttryckt i den beroende variabelns skala. Det kan alltså inte användas för att jämföra olika regressionsanalyser med varandra.
G	Här står namnet på den beroende variabeln, "realrinc".
H	Namnet på den oberoende variabeln, "hrs1". Har man fler oberoende variabler står de i egna rader under.
I	B-koefficienten för "hrs1", 458.4551. Det betyder att om vi ökar hrs1 med ett steg (alltså jobbar en timma mer i veckan) förväntas årsinkomsten öka med 458.4551 dollar.
J	Standardfelet för b-koefficienten för hrs1, som är ett mått på osäkerheten i uppskattningen. Ju större standardfelet är i förhållande till b-koefficienten, desto mindre säkra kan vi vara på att koefficienten i populationen (i det här fallet, amerikanska folket) verkligen är det som b-koefficienten säger.
K	t-värdet för hrs1. Det visar hur osannolikt det är att vi skulle få ett så här starkt samband mellan hrs1 och realrinc, om det inte fanns något ute i populationen som vi har gjort vårat urval ifrån. Ju högre t-värde, desto mer osannolikt. Är det väldigt osannolikt är det rimligare att dra slutsatsen att det finns ett samband mellan antal arbetade timmar och inkomst, även ute i populationen.
L	P-värdet, eller signifikansvärdet. Det visar i princip samma sak som t-värdet, fast uttryckt på ett lite annat sätt. Det visar hur ofta vi får ett så starkt samband mellan hrs1 och realrinc som vi nu har sett, bara på grund av slump i urvalet, om det inte skulle finnas något ute i populationen. I det här fallet är värdet 0.006, vilket innebär att även om det ute i befolkningen inte skulle finnas något samband mellan arbetade timmar och inkomst skulle vi uppmätta ett så här starkt samband 6 gånger av tusen, bara på grund av slump, om vi gör slumpmässiga urval av 46 personer. Vanligtvis brukar beslutsgränsen vara 0.05 - är signifikansvärdet under 0.05 säger vi att resultatet är statistiskt signifikant på 95%-nivån. Vi drar då slutsatsen att det finns ett samband mellan variablerna även ute i populationen.
M	Konfidensintervall för b-koefficienten för hrs1. Standardfelet visar att det finns en osäkerhet kring uppskattningen av vad b-koefficienten är. Konfidensintervallet visar det lite mer intuitivt. Vi kan inte vara säkra på att b-koefficienten är just 458, men vi kan vara rätt säkra på att den är något mellan 139.66 och 777.25. 95%-konfidensintervallet är konstruerat så att om vi gör om undersökningen 100 gånger kommer konfidensintervallet täcka det sanna värdet 95 av 100 gånger. Om konfidensintervallet inte täcker 0 är p-värdet alltid under 0.05.
N	En beteckning på interceptet, det vill säga det värde vi gissar att den beroende variabeln ska ha om alla de oberoende variablerna är noll - i det här fallet att man jobbar noll timmar i veckan.
O	Värdet på interceptet - de som inte jobbar alls förväntas tjäna 2561 dollar per år, i genomsnitt.

Övriga värden på interceptets rad motsvarar saker som b-koefficienten för hrs1, det vill säga standardfel, t-värde, signifikansvärde och konfidensintervall. Men de har sällan någon teoretisk betydelse och tolkas sällan.

En grafisk jämförelse

Vi kan också titta på ett spridningsdiagram som visar regressionsanalysen. Några av sakerna vi ser i outputen ser vi också i diagrammet, de har betecknats på samma sätt:

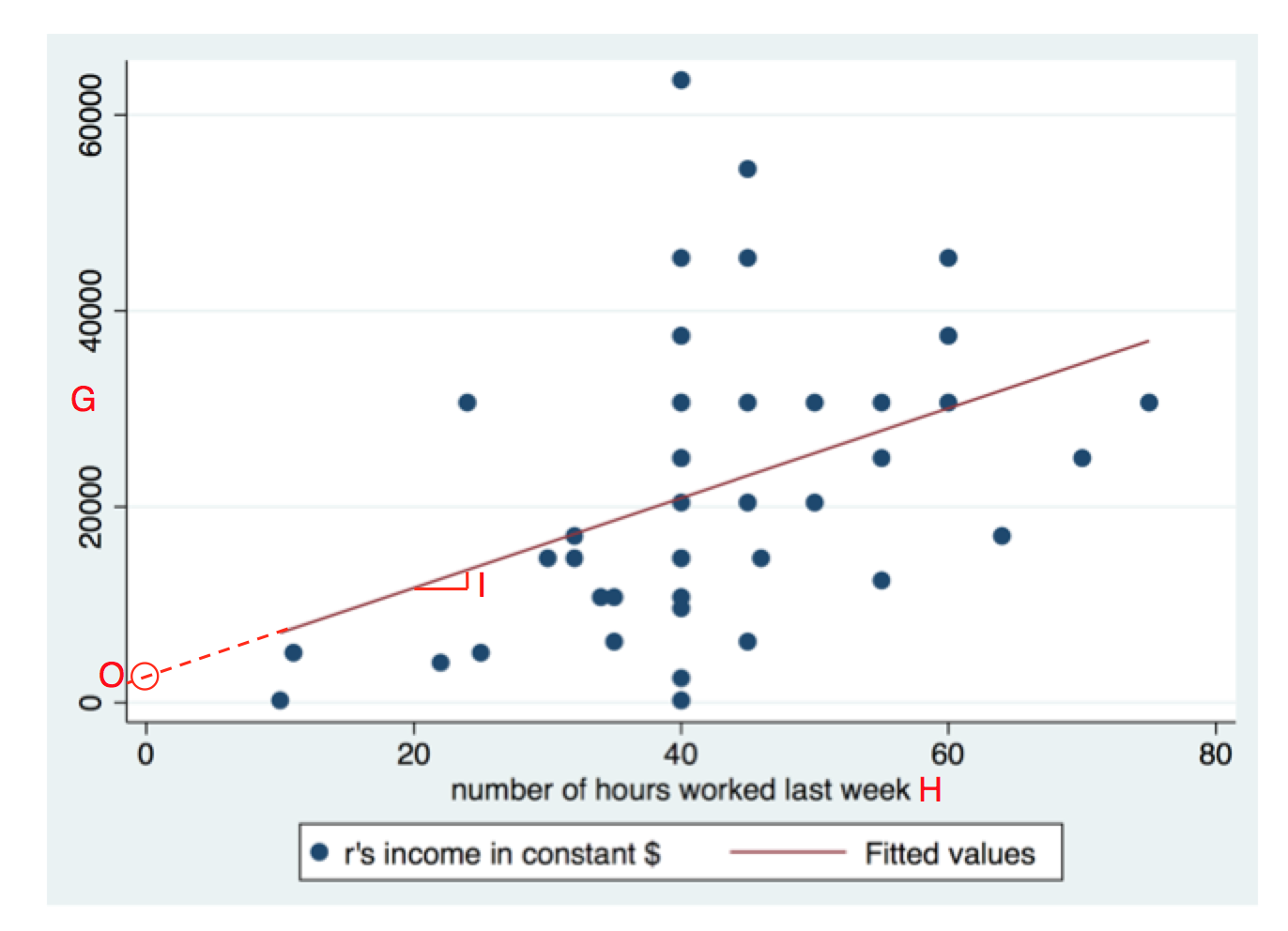
På y-axeln ser vi G, alltså den beroende variabeln. Den oberoende variabeln hrs1 hittar vi på x-axeln, betecknad med ett H. Varje person är en prick (det är något färre än 46 prickar, eftersom flera personer har samma värden och alltså befinner sig på samma plats).

B-koefficienten för hrs1 betecknades i tabellen med I, och här visas den som lutningen på regressionslinjen. När vi tar ett steg åt höger hamnar vi 458.4551 steg uppåt.

Interceptet (betecknat O) i tabellen hittar vi där regressionslinjen passerar nollan på X-axeln. Det vill säga, den gissade inkomsten för en person som jobbade noll timmar förra veckan. Någon sådan person fanns inte, men det spelar ingen roll.

$R^2$-värdet och standardfelet för b-koefficientent bestäms båda av prickarnas spridning kring regressionslinjen. Ju större spridning i förhållande till lutningen, desto större standardfel och desto lägre $R^2$-värde.

Avslutning

Det var det hela! När man har fler oberoende variabler går det inte att lika direkt översätta analysen till ett tvådimensionellt spridningsdiagram, men principen är densamma. B-koefficienten innebär fortfarande hur mycket vi tror att den beroende variabeln kommer att öka om vi ökar den oberoende variabeln med ett steg, fast nu under kontroll för alla de andra oberoende variablerna.